Interest in exploiting the spin degree of freedom in semiconductors for both classical and quantum information processing is fueled by the promise of new devices with improved speed and functionality. The ability of spin to exist in superpositions of eigenstates is at the heart of recent proposals for spin-based "quantum bits" comprising quantum dots and nuclear spins. Experimental realizations of useful computation based on such units relies on the ability to perform a large number (>104) of single and multiple quantum bit operations within the limit imposed by the spin coherence time. In addition to efforts aimed at optimizing spin coherence times for such pursuits, recent experiments have shown that optical methods for producing ultrafast coherent spin rotations are also possible. This development may eventually enable one to perform millions of operations on quantum bits within typical coherence times. The mechanism for this process relies on the generation of an effective magnetic field by a below-bandgap laser pulse through the optical Stark effect. This field is used in lieu of conventional microwave fields to coherently rotate electron spins up to π/2 radians within the laser pulse duration (150fs). The rotations were measured as a reduction in the amplitude of spin precession initiated by a prior pump pulse.
Measurements of Stark shifts using time-resolved absorption
First observed in atoms, the optical Stark effect for excitonic transitions in semiconductors results from virtual excitations induced by intense pulses of sub-resonant photons. The end result is a shift of the absorption spectrum toward higher energy that lasts for the duration of the pump-probe correlation time (200-500 fs). This shift can be directly measured with time-resolved absorption techniques utilizing a spectrally broad probe pulse. For these experiments, an optical parametric amplifier produces tunable pump pulses and probe pulses of a white light continuum. Absorption spectra are taken at each value of pump-probe time delay using a photodiode array detector. After appropriate correction of the chirp present in such white light continua, spectra taken at negative, zero, and positive time delays can be compared to directly give the Stark shift.


This figure shows absorption spectra of an undoped ZnCdSe quantum well sample, directly resolving a Stark shift of the hh-exciton peak obtained with co-circularly polarized pump and probe pulses. Ep=2.3787 eV, Ip=0.65 GW/cm2.
Mechanism for coherent spin rotation
The dependence of the Stark shift on the relative polarizations of the pump and probe can be predicted from optical selection rules familiar for ordinary optical transitions. As a result, a σ+ polarized sub-resonant pump couples more strongly to σ+ hh-excitons than to σ+ lh-excitons. This results in a spin splitting of the conduction band that can be described as an effective magnetic field, HStark. Measurements of shifts for co- and counter-polarized probe pulses can be used to calculate the net conduction-band spin splitting, giving an effective magnetic field strength that reaches 20T for non-magnetic samples.
Shifts of conduction and valence band levels in a zinc-blende type semiconductor quantum well pro-duced by a below-bandgap, σ+-polarized pump pulse. The different shifts measured by co- (σ+) and counter-polarized (σ-) probe pulses at Ehh are primarily due to optical transition matrix elements.

Ultrafast manipulation of electron spins
In order for HStark to act upon electron spins, there must be a nonzero torque between the spin magnetization and the effective field. This is achieved at specific points in the spin precession cycle where S lies along the y-axis, corresponding to zero crossings in the detected Faraday rotation. For rotation angles θtip≠π, HStark acts to rotate the spin vector out of the plane of observation; subsequent spin precession then describes a cone around H0. Since only Sx is measured with the Faraday rotation technique, the spin rotation appears as a reduced amplitude of spin precession. θtip can then be calculated from the relation θtip=arccos(A/A0) , where A and A0 are the amplitudes of spin precession with and without HStark.
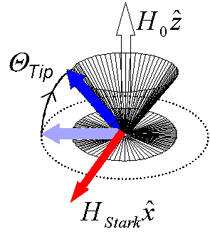
For these measurements, two synchronized optical parametric amplifiers are needed, since independently tunable pump and "Tipping pump" (TP) pulses must be used. The pump excites spin-polarized electrons and is tuned above the semiconductor bandgap, while the TP is tuned below the bandgap, in order to produce HStark. The spin dynamics are then measured through the Faraday rotation of a probe pulse consisting of a white light continuum.

This figure shows coherent spin rotations caused by the TP, with θtip> π/2, as evidenced by the change in sign of oscillations following the TP arrival (denoted by the red arrow). The black curve represents data taken without the TP as a measure of A0. Data were taken on a ZnCdMnSe magnetic quantum well.
