A lot of attention has been focused on zinc oxide (ZnO) because of material properties that make it well-suited for applications in ultra-violet light emitters, transparent high-power electronics and piezoelectric transducers. In addition, recent theoretical work, predicting room temperature ferromagnetism for Mn-doped p-type ZnO, has revealed the possibility that ZnO may be an appropriate candidate for spintronics, combining the functionalities of both semiconductors and magnetic materials. We investigate the electron spin dynamics of non-magnetically doped n-type ZnO using time-resolved Faraday rotation (TRFR), an optical pump-probe spectroscopic technique.

Commercially available high quality ZnO wafers (Courtesy: TEW, Tokyo-Denpa Ltd.)

First, we study 100 nm thick epitaxial thin films of ZnO, fabricated by pulsed laser deposition (PLD). The oxygen pressure used during the growth process for the epilayers tunes the carrier concentration, and we find that for the three samples measured, the spin lifetime (T2*) increases with increasing carrier density (fig. 1, left), from 0.5 ns (black) to 2.1 ns (blue). The Larmor precession frequency, ωL, increases linearly with magnetic field B in all the samples (fig. 1, right, bottom) and we extract a field-independent value of g* = 1.9 for the three epilayers. T2* decreases by almost 60% when the magnetic field is increased from B = 0.1 T to 1 T for the two samples with higher carrier concentration, and by about 30% for the least doped one (right, top)

Figure 1 Time-resolved Faraday rotation in PLD epilayer samples

We perform a detailed study of the temperature dependence of T2* in the sample with the highest carrier concentration, which has the longest spin coherence time of all the epilayers. Figure 2 (left) shows the TRFR response at B = 0.8 T for temperatures T = 80 K and 280 K. The g-factor g* is temperature independent t, while T2* decreases with increasing T. Remarkably, spin coherence persists until room temperature, with a spin lifetime of 188 ps at 280 K. shown on the right is a logarithmic plot of T2* as a function of T. Between 30 K and150 K, the spin coherence time follows a power law T -α, with α = 1.54 ± 0.03.

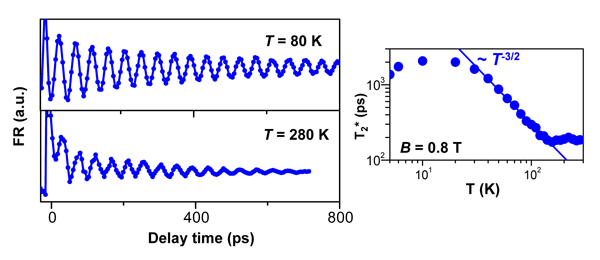
Figure 2 Temperature dependence of spin coherence time, exhibiting spin precession at high temperatures

We also measured a commercially purchased bulk single crystal from Tokyo-Denpa Company Ltd., grown by hydrothermal method. The carrier density in this sample was ~ 1015 cm-3, several orders of magnitude lower than that of the epilayers. However, the Faraday signal exhibits oscillations at negative delay (fig.3. top). This is indicative of spin magnetization persisting from the previous pump pulse, suggesting a long spin lifetime – greater than the repetition rate of the pulsed laser (13 ns), to be precise. We employ the method of resonant spin amplification (RSA) which makes it possible to measure spin coherence times well in excess of the laser repetition rate. Here, the Faraday rotation is measured at a fixed pump-probe delay. By varying the magnetic field and, thus, the Larmor frequency, resonant enhancements in Faraday rotation occur when the spin precession and pulse repetition periods are commensurate, due to constructive interference of successively excited spin packets. We see multiple RSA peaks in a magnetic field scan from +10 mT to – 10 mT (bottom, left). From a Lorentzian fit to the zero-field resonance peak, we obtain a T2* of 20 ns.

Figure 3 Faraday rotation in bulk single crystal showing surprisingly long spin coherence times

At the bottom right we show a log-log plot of the temperature dependence of T2* in the bulk sample obtained from such fits for 5 K < T < 100 K. For comparison, we reproduce the temperature dependence of the epilayer sample, and notice that despite having lower carrier concentration, T2* is larger by a factor of ten in the bulk. We speculate that these differences between the bulk and the epilayer may be attributed to the presence of compressive strain and higher density of defects in the latter.

To learn more about our studies, please refer to "Room temperature spin precession in ZnO", S. Ghosh et al., Appl. Phys. Lett., 86, 232507 (2005).