In order to comprehensively study the spin dynamics of a two-level quantum system, it is critical to calibrate each eigenstate. In the case of nitrogen vacancy (NV) centers in diamond, we calibrate the photoluminescence intensity (IPL) for each spin eigenstate to accurately determine the ms = 0 and ms = -1 population (P).

We employ an adiabatic passage to produce a precise spin-flip that is independent of the Rabi oscillation. This is done by applying a moderate driving field with a frequency strongly de-tuned from the spin resonance and subsequently sweeping the frequency adiabatically through the resonance causing the spin to flip. This procedure can be mapped as a Landau-Zener transition in the rotating frame with the probability of remaining in the ms = 0 state given by the Landau-Zener formula:

where H1 is the amplitude of the driving microwave field in units of the on-resonance Rabi frequency, and  is the Landau velocity, or sweep rate of the frequency.

To verify our adiabatic passage calibration, we measure IPL as we sweep through the ms = 0 to ms = -1 transition. For this measurement, we hold H1 constant at 29 MHz and sweep 300 MHz with various sweep durations to vary the Landau velocity. The result is shown below.

The data are fit to a simple exponential decay (red line) with a decay constant of 0.020 ± 0.001 ns-1, close to calculated value of 0.018 ns-1 given by the Landau-Zener formula. Next we fix the sweep duration to 600 ns ( = 0.5 MHz/ns), well into the adiabatic regime, and perform partial adiabatic passages. We stop the experiment at increasingly longer times and project the spin to see the progress of the spin-flip, shown below.

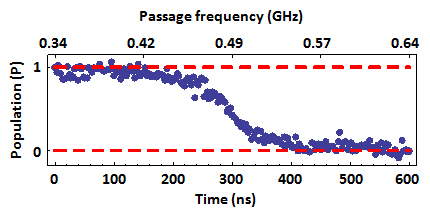
As expected, the spin flips as the driving frequency passes through resonance. In our work on strongly-driven NV centers, we use this technique to calibrate the measured IPL level with the value of P = 1 defined after initialization and P = 0 after adiabatic passage.

To learn more about our studies, please refer to "Gigahertz Dynamics of a Strongly Driven Single Quantum Spin", G. D. Fuchs, V. V. Dobrovitski, D. M. Toyli, F. J. Heremans, and D. D. Awschalom, Science 326, 1520 (2009).