The nitrogen vacancy (NV) center in diamond is a promising defect center for quantum information processing applications. Recent advances in chemical vapor deposition (CVD) diamond synthesis allow for precise doping of nitrogen with nanometer control of doping layer thickness, capable of hosting single, highly coherent NV center spins. While some nitrogen dopants are converted to NV centers, many remain as spin-1/2 particles that are a dominant—albeit unavoidable—source of decoherence. Furthermore, the stochastic nature of material growth causes variation in the local nitrogen environment (spin bath) of each NV center. Spin decoherence is very sensitive not just to the surrounding spin density, but to the couplings to nearby spins, dictated by their exact locations. Thus stochastic nitrogen incorporation naturally leads to variations in NV center coherence. While NV ensemble coherence in 3D spin baths is well understood, there is only sparse data available for single NV centers in 2D spin baths, a regime relevant for our NV synthesis. Here we sought to explore computationally coherence in 2D spin baths, uncovering dimensionality-dependent behavior that will guide future synthesis and developing a new in situ materials characterization technique.

We perform cluster correlation expansion (CCE) calculations on spin baths with parameters accessible in our CVD growth, shown schematically in the diamond heterostructure below. Isotopically pure diamond (to remove nuclear spin noise) is grown at 10s of nm/hr on a single crystal substrate, and nitrogen is controllably doped with a given density and layer thickness. CCE calculations consider a central spin, here a NV center in the nitrogen doped layer, surrounded by a spin bath, here unconverted N spins. CCE calculates the spin-conserving spin bath evolution and the resulting central spin decoherence.

We calculate single NV center coherences for standard T2* and T2 experiments, characterizing the coherence distributions with their log-mean and log-standard deviation. In this way we can compare the distributions across different scales. Our results map out the expected coherence yield across a range of parameter space, information that is both useful for future device synthesis and difficult to acquire experimentally. In both sets of calculations we observe trends towards higher coherence times in low-D spin baths, as well as a universal dependence of the distribution width (measured by the log-standard deviation) on the dimensionality. Our predicted T2 times are longer than experimentally observed, pointing towards other noise sources to be accounted for in future calculations.

We then apply our dataset as a characterization tool to non-destructively measure the spin bath (and thus nitrogen incorporation) geometry with NV coherence measurements. We measure single NV coherences in a test sample and perform a maximum likelihood estimation (MLE) to identify the most likely underlying bath parameters based on our calculated dataset. With only T2* measurements we fix the growth thickness and identify the nitrogen spin density. By performing the MLE with multiple types of coherence measurements, which probe different numbers of nearby spins, we demonstrate theoretically that one can identify both the thickness and density. We also show that the error in the density estimate drops approximately as 1N for N measure coherence times, reaching a modest error or 20% with only 10 measurements.

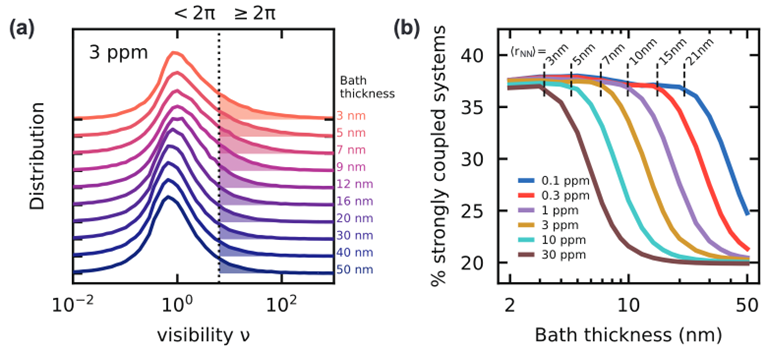
Finally, we computationally explore the occurrence of strongly coupled spin pairs in low-dimensional spin baths. Spins strongly coupled to NV centers may be advantageous for sensing and communication protocols. By varying the bath geometry, we find that when the spin bath is thinner than the average nearest-neighbor distance (when it enters a 2D regime) the number of strongly coupled spins, parametrized by the spin visibility, nearly doubles, pointing towards benefits of engineering spins in low dimensions.

Details can be found in our manuscript: 

J. C. Marcks, M. Onizhuk, N. Delegan, Y.-X. Wang, M. Fukami, M. Watts, A. A. Clerk, F. J. Heremans, G. Galli, D.D. Awschalom, Phys. Rev. Mat., 8, 026204 (2024).